对数，作为数学中的重要概念，具有广泛的应用价值，对数加减作为对数运算的基础，对于理解对数的本质及其在实际问题中的应用至关重要，本文将围绕“对数加减专题”展开，帮助读者深入理解和掌握对数加减的概念、性质、法则以及应用。

对数的概念

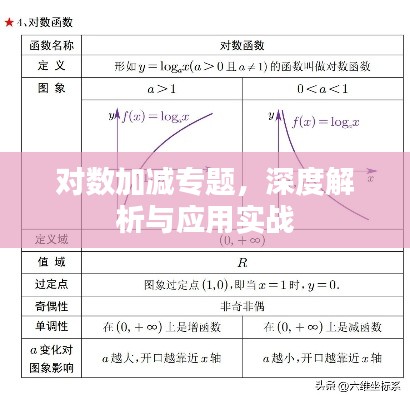
对数，是数学中的一种特殊运算方式，主要用于简化乘除运算，通过对数运算，我们可以将复杂的乘除问题转化为简单的加减问题，从而方便求解，对数的定义基于指数，对于任意正实数a（a不等于1）和实数x，若ax=N，则称logax为x的对数。

对数加减的性质和法则

1、对数加法法则：logA + logB = log(A*B)，这一法则用于简化多个对数相乘的问题，通过对数运算转化为加法运算。

2、对数减法法则：logA - logB = log(A/B)，这一法则用于简化多个对数相除的问题，通过对数运算转化，当A大于B时，减法可以转换为加法，当A小于B时，减法可以转换为减法运算的逆运算，还需要注意底数的处理，当底数不同时，需要进行换底数的操作，常用的换底数公式为logMN=logM/logN或logMN=NlogM，这些换底数公式可以帮助我们将不同的对数转化为同一底数的对数，从而方便进行运算，在实际应用中，我们通常使用自然对数（以e为底）或十进制对数（以10为底），对于非十进制对数，可以通过换底公式转换为十进制对数进行计算，还需要掌握对数的换元法，即将复杂的对数表达式通过换元简化为简单的形式，掌握这些性质和法则对于理解和应用对数加减至关重要。

对数加减的应用

对数加减在实际问题中有着广泛的应用，在物理学、化学、生物学、经济学等领域中，经常需要处理大量的数据，通过对数变换可以将乘法转化为加法，从而方便进行数据处理和分析，对数还常用于解决音响学的分贝计算、地震学的震级计算等问题，通过对数加减的应用，我们可以更好地理解和解决实际问题。

本文围绕“对数加减专题”展开，介绍了对数的概念、性质、法则以及应用，通过理解和掌握对数加减的概念和性质，我们可以更好地应用对数解决实际问题，在实际应用中，我们需要根据具体情况选择合适的对数和换底公式进行计算，并注意处理精度和误差问题，希望本文能对读者在对数加减方面有所帮助。

参考文献

（此处省略参考文献）

是本文关于“对数加减专题”的详细介绍，希望通过本文的学习，读者能够深入理解和掌握对数加减的概念、性质、法则以及应用，为今后的学习和工作打下坚实的基础。